“Mathematics is the art of reducing any problem to linear algebra.” — William Stein

If you’ve ever looked at a vector and thought, “Just a column of numbers, right?”, this chapter will change that. The Dark Art of Linear Algebra (aka DALA) by Seth Braver opens with one of the clearest intros I’ve read. Not every part clicks on the first pass, but the effort pays off. Paired with the author’s videos, this is a strong starting point whether you’re learning math for the first time or coming back to it with purpose.

As I wrote in Unlocking AI with Math and [Book Notes] Infinitesimals, Derivatives, and Beer – Full Frontal Calculus (Ch. 1), I’m not learning math to pass a test. I’m learning it to understand the machinery behind AI and robotics, and eventually build machines of my own. (That would be fun, right?)

That goal needs a solid grasp of linear algebra. And it starts with understanding what a vector really is. Not just how to work with vectors algebraically, but how they behave in space and fit into a larger structure.

This chapter helped me sharpen that understanding.

Chapter Notes

What’s a Vector?

The book makes it clear that the answer to this question will evolve as you go deeper into linear algebra. But Chapter 1 starts simple: a vector is an arrow. A geometric object. A displacement.

In the video that comes with the chapter, the author even says to forget everything you think you know about vectors. He introduces them geometrically, which makes them feel tangible and helps you see familiar algebraic ideas in a visual, spatial way.

Vector Addition

The book introduces vector addition visually. Once you see vectors as displacements or moves through space, the addition feels natural. Almost obvious.

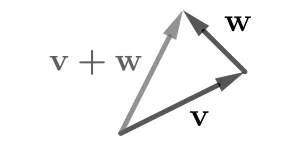Image source: DALA Ch1

The text doesn’t focus on vector subtraction, but there’s an exercise on it. The companion video shows two methods. One of them is subtraction by addition: flip the direction of the vector you want to subtract, then add. It reminded me of that Office scene where Andy says “addition by subtraction,” and Michael asks, “What does that even mean?” In that context, it’s just a throwaway phrase. But in vector math, subtraction by addition is a real method. Flip the vector, then add. If you’ve done engineering, you’ve likely seen this before.

Vector addition also follows familiar rules like commutativity and associativity. If those sound fuzzy, the book and video prove them using triangles and parallelograms. No heavy algebra, just geometry.

One nice bonus is that the commutative proof gives you another way to add vectors. Place both tails at the same point, draw a parallelogram, and the diagonal gives the sum. Itss clean and easy to visualize:

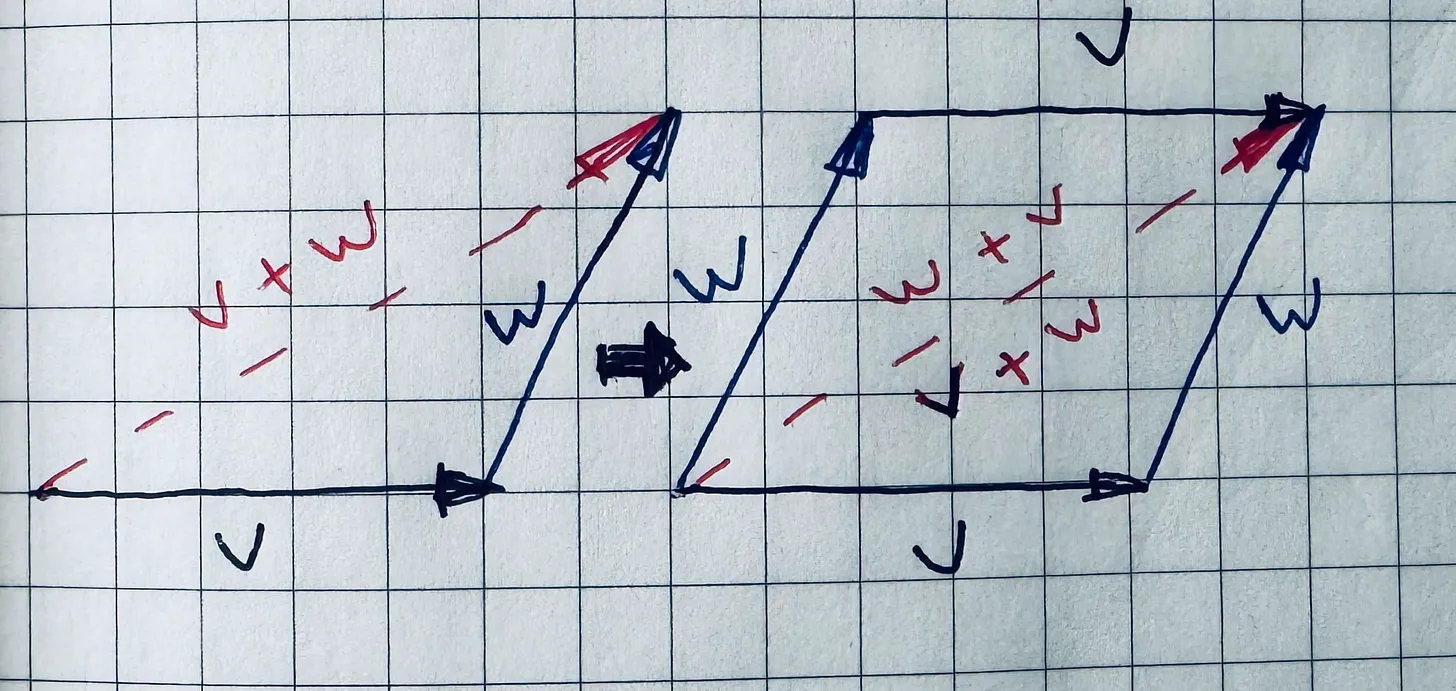
Stretching Vectors

Scalar multiplication is introduced as a way to stretch, shrink, or flip a vector, not just multiply its components.

The author even explains where the word scalar comes from. Numbers are called scalars because they scale vectors. I liked that he doesn’t assume you already know this.

To stretch a vector, multiply by 3.

To flip it, multiply by –1.

To collapse it, multiply by 0.

It’s easier to remember when you learn it by drawing instead of just computing.

Standard Basis Vectors

Only after you’ve built a solid geometric understanding does the author introduce the standard basis vectors: i, j, and k. By then, it’s clear that 2i + 3j + 5k is just a weighted sum of familiar directions.

The chapter shows how to express vectors in ℝ² and ℝ³ using these basis vectors, and how to rewrite them in column form.

Length of Vectors

Be sure to watch the videos that go with this chapter. They walk you through finding the length of a vector visually.

You’ll start with the Pythagorean theorem to calculate the length of a vector in ℝ³, then extend the idea to ℝⁿ. The chapter also proves the general length formula when a vector is written in Cartesian coordinates. Neat.

The Dot Product

The chapter defines the dot product using the same geometric approach as earlier sections, and it makes sense. But for me, it really clicked in the physics example where work is defined using the dot product. The author’s video made it even clearer.

In the screenshot above, I underlined “Thus we see that work, viewed in a more general setting, is simply a dot product” and scribbled “watch the video” in the margin. Just a reminder that the video is a great companion to the chapter.

The text then walks through key properties: commutativity, dotting a vector with itself, the distributive property, a test for perpendicularity, and how to compute the dot product in ℝ².

You could memorize the formula. But it’s much more satisfying to understand the parts and derive it from scratch. Like Einstein said, “Any fool can know. The point is to understand.”

Here’s a step-by-step derivation, written out in my notes:

Thoughts and Tips

Like Full Frontal Calculus did for derivatives, this chapter tears vectors down to the basics and builds them back up. It does that visually, intuitively, and from first principles. It starts with geometry, not formulas. By the end, it’s clear that coordinates are just a way to describe vectors. They are not the vectors themselves.

Verdict: Highly recommend if you want a clear, visual grasp of what vectors really are. Especially if linear algebra has ever felt abstract, dry, or overly symbolic.

If you plan to read the chapter, these tips helped me get the most out of it:

1. Read slowly. Then read slowly again. The material is clear, but it rewards focused attention. Grab a paperback if you can. Write in the margins. Make the book your own.

2. Watch the author’s YouTube videos. The book explains the idea. The video often makes it stick. If you’re reading any of Braver’s math books, don’t skip the videos. They’re short, clear, and worth it.

   1. Vectors (from a geometric perspective)
   2. The Dot Product (from a geometric perspective)

3. Don’t worry about the proofs. They’re explained in plain language, supported by visuals, and still rigorous. You don’t need a separate book on how to follow them. They just make sense.

4. Brush up on your trig. Knowing how cosine works pays off when finding angles between vectors. It’s a small part of the chapter, but if you’re rusty, check out the trig section in Precalculus Made Difficult by the same author.

5. Do the exercises. The book includes answers, which makes it great for self-study. But like in Full Frontal Calculus, the solutions are compact. Use ChatGPT or Grok (xAI) to expand on them when needed.

6. Use spaced repetition. For ideas that are hard to keep in memory, try active recall. I use Anki, but any similar tool should work.

7. Check out the book sample. The author offers a sample on his site. If you’re on the fence, it gives you a solid feel for the writing and style.

These pages and videos are exactly what I wish I had the first time I saw vectors. They make the concept click and give you a foundation you can build on, whether you’re starting fresh or coming back to review.

More to come. Stay tuned.

Originally published in my newsletter Beyond Basics. If you’d like to get future posts like this by email, you can subscribe here.

P.S. I’m not affiliated with the author. I just really enjoy his books and wanted to share that.

Get the edge and stay sharp. Subscribe to Beyond Basics for free and get new posts without missing a beat!