Let’s Build A Simple Interpreter. Part 13: Semantic Analysis.

Date

Anything worth doing is worth overdoing.

Before doing a deep dive into the topic of scopes, I’d like to make a “quick” detour and talk in more detail about symbols, symbol tables, and semantic analysis. In the spirit of “Anything worth doing is worth overdoing”, I hope you’ll find the material useful for building a more solid foundation before tackling nested scopes. Today we will continue to increase our knowledge of how to write interpreters and compilers. You will see that some of the material covered in this article has parts that are much more extended versions of what you saw in Part 11, where we discussed symbols and symbol tables.


Okay, let’s get started!


Introduction to semantic analysis

While our Pascal program can be grammatically correct and the parser can successfully build an abstract syntax tree, the program still can contain some pretty serious errors. To catch those errors we need to use the abstract syntax tree and the information from the symbol table.

Why can’t we check for those errors during parsing, that is, during syntax analysis? Why do we have to build an AST and something called the symbol table to do that?

In a nutshell, for convenience and the separation of concerns. By moving those extra checks into a separate phase, we can focus on one task at a time without making our parser and interpreter do more work than they are supposed to do.

When the parser has finished building the AST, we know that the program is grammatically correct; that is, that its syntax is correct according to our grammar rules and now we can separately focus on checking for errors that require additional context and information that the parser did not have at the time of building the AST. To make it more concrete, let’s take a look at the following Pascal assignment statement:

x := x + y;


The parser will handle it all right because, grammatically, the statement is correct (according to our previously defined grammar rules for assignment statements and expressions). But that’s not the end of the story yet, because Pascal has a requirement that variables must be declared with their corresponding types before they are used. How does the parser know whether x and y have been declared yet?

Well, it doesn’t and that’s why we need a separate semantic analysis phase to answer the question (among many others) of whether the variables have been declared prior to their use.

What is semantic analysis? Basically, it’s just a process to help us determine whether a program makes sense, and that it has meaning, according to a language definition.

What does it even mean for a program to make sense? It depends in large part on a language definition and language requirements.

Pascal language and, specifically, Free Pascal’s compiler, has certain requirements that, if not followed in a program, would lead to an error from the fpc compiler indicating that the program doesn’t “make sense”, that it is incorrect, even though the syntax might look okay. Here are some of those requirements:

  • The variables must be declared before they are used
  • The variables must have matching types when used in arithmetic expressions (this is a big part of semantic analysis called type checking that we’ll cover separately)
  • There should be no duplicate declarations (Pascal prohibits, for example, having a local variable in a procedure with the same name as one of the procedure’s formal parameters)
  • A name reference in a call to a procedure must refer to the actual declared procedure (It doesn’t make sense in Pascal if, in the procedure call foo(), the name foo refers to a variable foo of a primitive type INTEGER)
  • A procedure call must have the correct number of arguments and the arguments’ types must match those of formal parameters in the procedure declaration

It is much easier to enforce the above requirements when we have enough context about the program, namely, an intermediate representation in the form of an AST that we can walk and the symbol table with information about different program entities like variables, procedures, and functions.

After we implement the semantic analysis phase, the structure of our Pascal interpreter will look something like this:

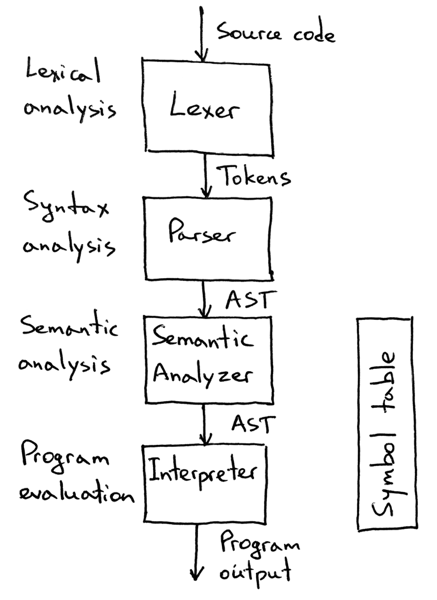
From the picture above you can see that our lexer will get source code as an input, transform that into tokens that the parser will consume and use to verify that the program is grammatically correct, and then it will generate an abstract syntax tree that our new semantic analysis phase will use to enforce different Pascal language requirements. During the semantic analysis phase, the semantic analyzer will also build and use the symbol table. After the semantic analysis, our interpreter will take the AST, evaluate the program by walking the AST, and produce the program output.

Let’s get into the details of the semantic analysis phase.

Symbols and symbol tables

In the following section, we’re going to discuss how to implement some of the semantic checks and how to build the symbol table: in other words, we are going to discuss how to perform a semantic analysis of our Pascal programs. Keep in mind that even though semantic analysis sounds fancy and deep, it’s just another step after parsing our program and creating an AST to check the source program for some additional errors that the parser couldn’t catch due to a lack of additional information (context).

Today we’re going to focus on the following two static semantic checks*:

  1. That variables are declared before they are used
  2. That there are no duplicate variable declarations

*ASIDE: Static semantic checks are the checks that we can make before interpreting (evaluating) the program, that is, before calling the interpret method on an instance of the Interpreter class. All the Pascal requirements mentioned before can be enforced with static semantic checks by walking an AST and using information from the symbol table.

Dynamic semantic checks, on the other hand, would require checks to be performed during the interpretation (evaluation) of the program. For example, a check that there is no division by zero, and that an array index is not out of bounds would be a dynamic semantic check. Our focus today is on static semantic checks.

Let’s start with our first check and make sure that in our Pascal programs variables are declared before they are used. Take a look at the following syntactically correct but semantically incorrect program (ugh… too many hard to pronounce words in one sentence. :)

program Main;
   var x : integer;

begin
    x := y;
end.

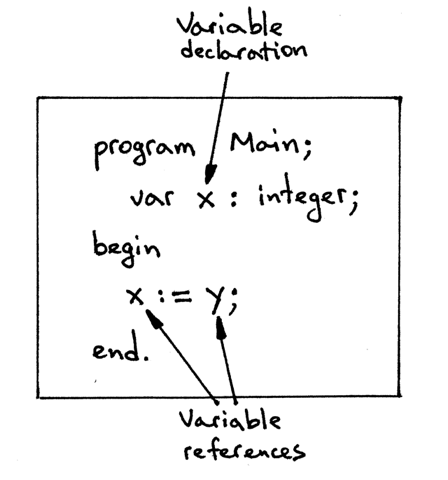
The program above has one variable declaration and two variable references. You can see that in the picture below:

Let’s actually verify that our program is syntactically correct and that our parser doesn’t throw an error when parsing it. As they say, trust but verify. :) Download spi.py, fire off a Python shell, and see for yourself:

>>> from spi import Lexer, Parser
>>> text = """
program Main;
   var x : integer;

begin
    x := y;
end.
"""
>>>
>>> lexer = Lexer(text)
>>> parser = Parser(lexer)
>>> tree = parser.parse()
>>>

You see? No errors. We can even generate an AST diagram for that program using genastdot.py. First, save the source code into a file, let’s say semanticerror01.pas, and run the following commands:

$ python genastdot.py semanticerror01.pas > semanticerror01.dot
$ dot -Tpng -o ast.png semanticerror01.dot

Here is the AST diagram:

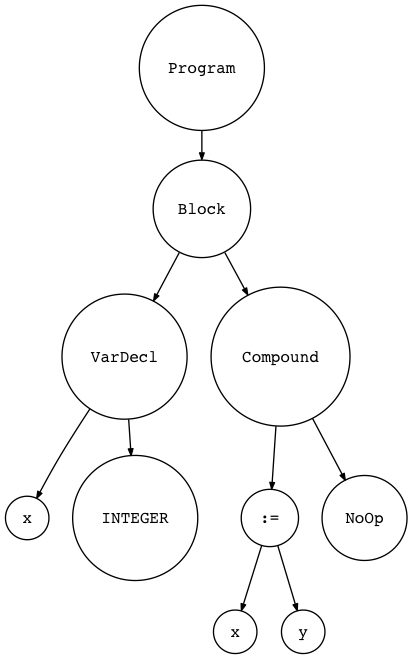
So, it is a grammatically (syntactically) correct program, but the program doesn’t make sense because we don’t even know what type the variable y has (that’s why we need declarations) and if it will make sense to assign y to x. What if y is a string, does it make sense to assign a string to an integer? It does not, at least not in Pascal.

So the program above has a semantic error because the variable y is not declared and we don’t know its type. In order for us to be able to catch errors like that, we need to learn how to check that variables are declared before they are used. So let’s learn how to do it.

Let’s take a closer look at the following syntactically and semantically correct sample program:

program Main;
   var x, y : integer;

begin
    x := x + y;
end.
  • It has two variable declarations: x and y
  • It also has three variable references (x, another x, and y) in the assignment statement x := x + y;

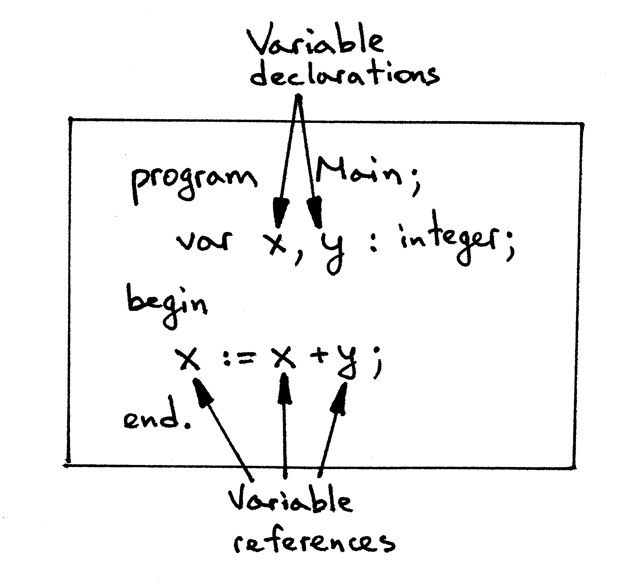
The program is grammatically correct, all the variables are declared, and we can see that adding two integers and assigning the result to an integer makes perfect sense. That’s great, but how do we programmatically check that the variables (variable references) x and y in the assignment statement x := x +y; have been declared?

We can do this in several steps by implementing the following algorithm:

  1. Go over all variable declarations
  2. For every variable declaration you encounter, collect all necessary information about the declared variable
  3. Store the collected information in some stash for future reference by using the variable’s name as a key
  4. When you see a variable reference, such as in the assignment statement x := x + y, search the stash by the variable’s name to see if the stash has any information about the variable. If it does, the variable has been declared. If it doesn’t, the variable hasn’t been declared yet, which is a semantic error.

This is what a flowchart of our algorithm could look like:

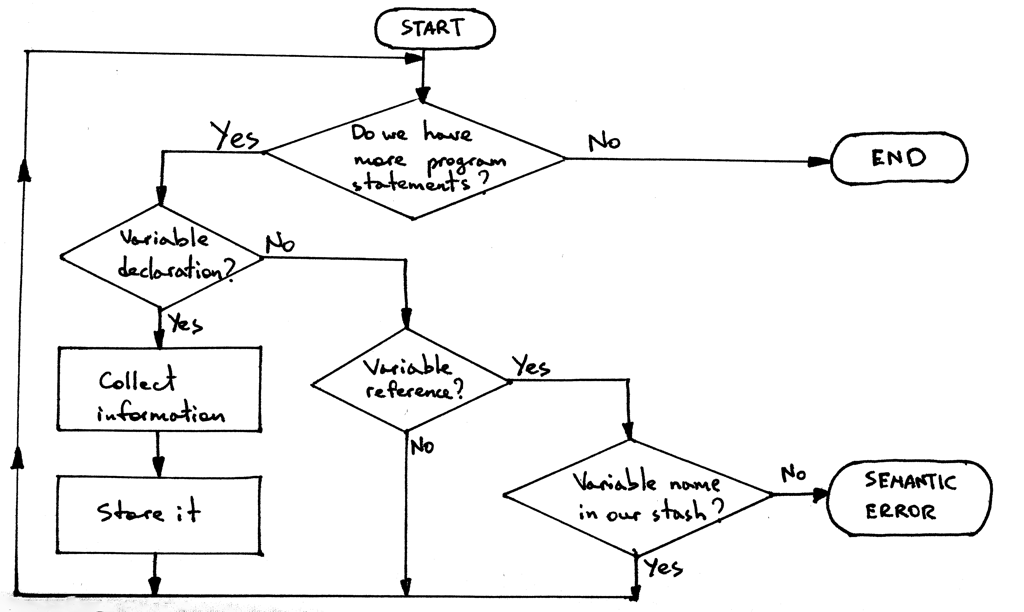
Before we can implement the algorithm, we need to answer several questions:

  • A. What information about variables do we need to collect?
  • B. Where and how should we store the collected information?
  • C. How do we implement the “go over all variable declarations” step?

Our plan of attack will be the following:

  1. Figure out answers to the questions A, B, and C above.
  2. Use the answers to A, B, and C to implement the steps in the algorithm for our first static semantic check: a check that variables are declared before they are used.

Okay, let’s get started.

Let’s find an answer to the question “What information about variables do we need to collect?”

So, what necessary information do we need to collect about a variable? Here are the important parts:

  • Name (we need to know the name of a declared variable because later we will be looking up variables by their names)
  • Category (we need to know what kind of an identifier it is: variable, type, procedure, and so on)
  • Type (we’ll need this information for type checking)

Symbols will hold that information (name, category, and type) about our variables. What’s a symbol? A symbol is an identifier of some program entity like a variable, subroutine, or built-in type.

In the following sample program we have two variable declarations that we will use to create two variable symbols: x, and y.

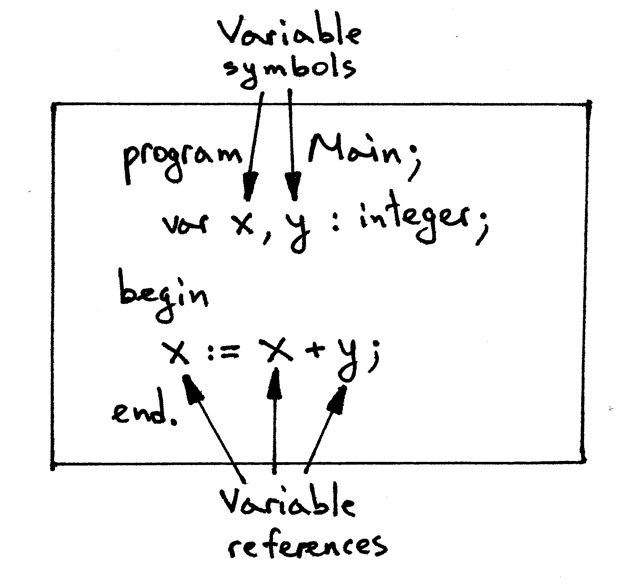
In the code, we’ll represent symbols with a class called Symbol that has fields name and type :

class Symbol(object):
    def __init__(self, name, type=None):
        self.name = name
        self.type = type

As you can see, the class takes the name parameter and an optional type parameter (not all symbols have type information associated with them, as we’ll see shortly).

What about the category? We will encode category into the class name. Alternatively, we could store the category of a symbol in the dedicated category field of the Symbol class as in:

class Symbol(object):
    def __init__(self, name, type=None):
        self.name = name
        self.type = type
        self.category = category

However, it’s more explicit to create a hierarchy of classes where the name of the class indicates its category.

Up until now I’ve sort of skirted around one topic, that of built-in types. If you look at our sample program again:

program Main;
   var x, y : integer;

begin
    x := x + y;
end.

You can see that variables x and y are declared as integers. What is the integer type? The integer type is another kind of symbol, a built-in type symbol. It’s called built-in because it doesn’t have to be declared explicitly in a Pascal program. It’s our interpreter’s responsibility to declare that type symbol and make it available to programmers:

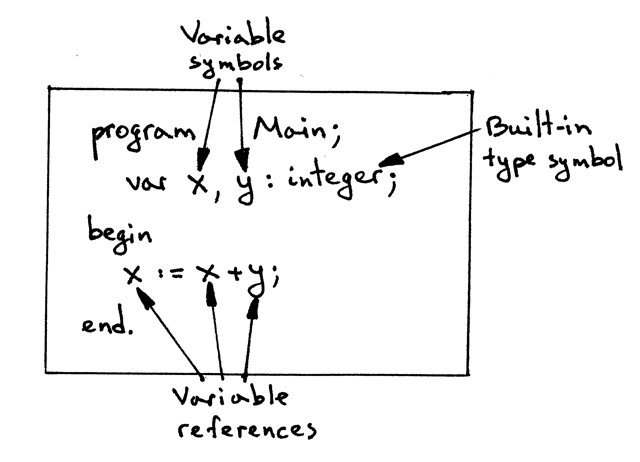
We are going to make a separate class for built-in types called BuiltinTypeSymbol. Here is the class definition for our built-in types:

class BuiltinTypeSymbol(Symbol):
    def __init__(self, name):
        super().__init__(name)

    def __str__(self):
        return self.name

    def __repr__(self):
        return "<{class_name}(name='{name}')>".format(
            class_name=self.__class__.__name__,
            name=self.name,
        )

The class BuiltinTypeSymbol inherits from the Symbol class, and its constructor requires only the name of the type, like integer or real. The ‘builtin type’ category is encoded in the class name, as we discussed earlier, and the type parameter from the base class is automatically set to None when we create a new instance of the BuiltinTypeSymbol class.

ASIDE

The double underscore or dunder (as in “Double UNDERscore”) methods __str__ and __repr__ are special Python methods. We’ve defined them to have a nice formatted message when we print a symbol object to standard output.

By the way, built-in types are the reason why the type parameter in the Symbol class constructor is an optional parameter.

Here is our symbol class hierarchy so far:

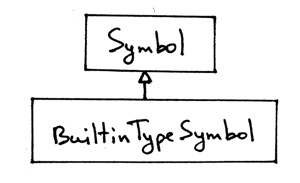
Let’s play with the builtin types in a Python shell. Download the interpreter file and save it as spi.py; launch a python shell from the same directory where you saved the spi.py file, and play with the class we’ve just defined interactively:

$ python
>>> from spi import BuiltinTypeSymbol
>>> int_type = BuiltinTypeSymbol('integer')
>>> int_type
<BuiltinTypeSymbol(name='integer')>
>>>
>>> real_type = BuiltinTypeSymbol('real')
>>> real_type
<BuiltinTypeSymbol(name='real')>

That’s all there is to built-in type symbols for now. Now back to our variable symbols.

How can we represent them in code? Let’s create a VarSymbol class:

class VarSymbol(Symbol):
    def __init__(self, name, type):
        super().__init__(name, type)

    def __str__(self):
        return "<{class_name}(name='{name}', type='{type}')>".format(
            class_name=self.__class__.__name__,
            name=self.name,
            type=self.type,
        )

    __repr__ = __str__

In this class, we made both the name and the type parameters required and the class name VarSymbol clearly indicates that an instance of the class will identify a variable symbol (the category is variable). The type parameter is an instance of the BuiltinTypeSymbol class.

Let’s go back to the interactive Python shell to see how we can manually construct instances of our variable symbols now that we know how to construct BuiltinTypeSymbol class instances:

$ python
>>> from spi import BuiltinTypeSymbol, VarSymbol
>>> int_type = BuiltinTypeSymbol('integer')
>>> real_type = BuiltinTypeSymbol('real')
>>>
>>> var_x_symbol = VarSymbol('x', int_type)
>>> var_x_symbol
<VarSymbol(name='x', type='integer')>
>>>
>>> var_y_symbol = VarSymbol('y', real_type)
>>> var_y_symbol
<VarSymbol(name='y', type='real')>
>>>

As you can see, we first create an instance of the built-in type symbol and then pass it as a second parameter to VarSymbol‘s constructor: variable symbols must have both a name and type associated with them as you’ve seen in various variable declarations like var x : integer;

And here is the complete hierarchy of symbols we’ve defined so far, in visual form:


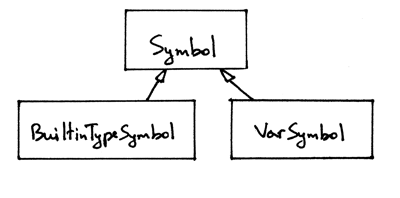
Okay, now onto answering the question “Where and how should we store the collected information?”

Now that we have all the symbols representing all our variable declarations, where should we store those symbols so that we can search for them later when we encounter variable references (names)?

The answer is, as you probably already know, in the symbol table.

What is a symbol table? A symbol table is an abstract data type for tracking various symbols in source code. Think of it as a dictionary where the key is the symbol’s name and the value is an instance of the symbol class (or one of its subclasses). To represent the symbol table in code we’ll use a dedicated class for it aptly named SymbolTable. :) To store symbols in the symbol table we’ll add the insert method to our symbol table class. The method insert will take a symbol as a parameter and store it internally in the _symbols ordered dictionary using the symbol’s name as a key and the symbol instance as a value:

class SymbolTable(object):
    def __init__(self):
        self._symbols = {}

    def __str__(self):
        symtab_header = 'Symbol table contents'
        lines = ['\n', symtab_header, '_' * len(symtab_header)]
        lines.extend(
            ('%7s: %r' % (key, value))
            for key, value in self._symbols.items()
        )
        lines.append('\n')
        s = '\n'.join(lines)
        return s

    __repr__ = __str__

    def insert(self, symbol):
        print('Insert: %s' % symbol.name)
        self._symbols[symbol.name] = symbol

Let’s manually populate our symbol table for the following sample program. Because we don’t know how to search our symbol table yet, our program won’t contain any variable references, only variable declarations:

program SymTab1;
   var x, y : integer;

begin

end.

Download symtab01.py, which contains our new SymbolTable class and run it on the command line. This is what the output looks like for our program above:

$ python symtab01.py
Insert: INTEGER
Insert: x
Insert: y


Symbol table contents
_____________________
INTEGER: <BuiltinTypeSymbol(name='INTEGER')>
      x: <VarSymbol(name='x', type='INTEGER')>
      y: <VarSymbol(name='y', type='INTEGER')>


And now let’s build and populate the symbol table manually in a Python shell:

$ python
>>> from symtab01 import SymbolTable, BuiltinTypeSymbol, VarSymbol
>>> symtab = SymbolTable()
>>> int_type = BuiltinTypeSymbol('INTEGER')
>>> # now let's store the built-in type symbol in the symbol table
...
>>> symtab.insert(int_type)
Insert: INTEGER
>>>
>>> symtab


Symbol table contents
_____________________
INTEGER: <BuiltinTypeSymbol(name='INTEGER')>


>>> var_x_symbol = VarSymbol('x', int_type)
>>> symtab.insert(var_x_symbol)
Insert: x
>>> symtab


Symbol table contents
_____________________
INTEGER: <BuiltinTypeSymbol(name='INTEGER')>
      x: <VarSymbol(name='x', type='INTEGER')>


>>> var_y_symbol = VarSymbol('y', int_type)
>>> symtab.insert(var_y_symbol)
Insert: y
>>> symtab


Symbol table contents
_____________________
INTEGER: <BuiltinTypeSymbol(name='INTEGER')>
      x: <VarSymbol(name='x', type='INTEGER')>
      y: <VarSymbol(name='y', type='INTEGER')>


>>>


At this point we have answers to two questions that we asked earlier:

  • A. What information about variables do we need to collect?

    Name, category, and type. And we use symbols to hold that information.

  • B. Where and how should we store the collected information?

    We store collected symbols in the symbol table by using its insert method.


Now let’s find the answer to our third question: ‘How do we implement the “go over all variable declarations” step?’

This is a really easy one. Because we already have an AST built by our parser, we just need to create a new AST visitor class that will be responsible for walking over the tree and doing different actions when visiting VarDecl AST nodes!

Now we have answers to all three questions:

  • A. What information about variables do we need to collect?

    Name, category, and type. And we use symbols to hold that information.

  • B. Where and how should we store the collected information?

    We store collected symbols in the symbol table by using its insert method.

  • C. How do we implement the “go over all variable declarations” step?

    We will create a new AST visitor that will do some actions on visiting VarDecl AST nodes.


Let’s create a new tree visitor class and give it the name SemanticAnalyzer. Take a look the following sample program, for example:

program SymTab2;
   var x, y : integer;

begin

end.

To be able to analyze the program above, we don’t need to implement all visit_xxx methods, just a subset of them. Below is the skeleton for the SemanticAnalyzer class with enough visit_xxx methods to be able to successfully walk the AST of the sample program above:

class SemanticAnalyzer(NodeVisitor):
    def __init__(self):
        self.symtab = SymbolTable()

    def visit_Block(self, node):
        for declaration in node.declarations:
            self.visit(declaration)
        self.visit(node.compound_statement)

    def visit_Program(self, node):
        self.visit(node.block)

    def visit_Compound(self, node):
        for child in node.children:
            self.visit(child)

    def visit_NoOp(self, node):
        pass

    def visit_VarDecl(self, node):
        #  Actions go here
        pass

Now, we have all the pieces to implement the first three steps of our algorithm for our first static semantic check, the check that verifies that variables are declared before they are used.

Here are the steps of the algorithm again:

  1. Go over all variable declarations
  2. For every variable declaration you encounter, collect all necessary information about the declared variable
  3. Store the collected information in some stash for future references by using the variable’s name as a key
  4. When you see a variable reference such as in the assignment statement x := x + y, search the stash by the variable’s name to see if the stash has any information about the variable. If it does, the variable has been declared. If it doesn’t, the variable hasn’t been declared yet, which is a semantic error.


Let’s implement those steps. Actually, the only thing that we need to do is fill in the visit_VarDecl method of the SemanticAnalyzer class. Here it is, filled in:

def visit_VarDecl(self, node):
    # For now, manually create a symbol for the INTEGER built-in type
    # and insert the type symbol in the symbol table.
    type_symbol = BuiltinTypeSymbol('INTEGER')
    self.symtab.insert(type_symbol)

    # We have all the information we need to create a variable symbol.
    # Create the symbol and insert it into the symbol table.
    var_name = node.var_node.value
    var_symbol = VarSymbol(var_name, type_symbol)
    self.symtab.insert(var_symbol)

If you look at the contents of the method, you can see that it actually incorporates all three steps:

  1. The method will be called for every variable declaration once we’ve invoked the visit method of the SemanticAnalyzer instance. That covers Step 1 of the algorithm: “Go over all variable declarations”
  2. For every variable declaration, the method visit_VarDecl will collect the necessary information and create a variable symbol instance. That covers Step 2 of the algorithm: “For every variable declaration you encounter, collect all necessary information about the declared variable”
  3. The method visit_VarDecl will store the collected information about the variable declaration in the symbol table using the symbol table’s insert method. This covers Step 3 of the algorithm: “Store the collected information in some stash for future references by using the variable’s name as a key”

To see all of those steps in action, download file symtab02.py and study its source code first. Then run it on the command line and inspect the output:

$ python symtab02.py
Insert: INTEGER
Insert: x
Insert: INTEGER
Insert: y


Symbol table contents
_____________________
INTEGER: <BuiltinTypeSymbol(name='INTEGER')>
      x: <VarSymbol(name='x', type='INTEGER')>
      y: <VarSymbol(name='y', type='INTEGER')>

You might have noticed that there are two lines that say Insert: INTEGER. We will fix this situation in the following section where we’ll discuss the implementation of the final step (Step 4) of the semantic check algorithm.


Okay, let’s implement Step 4 of our algorithm. Here is an updated version of Step 4 to reflect the introduction of symbols and the symbol table: When you see a variable reference (name) such as in the assignment statement x := x + y, search the symbol table by the variable’s name to see if the table has a variable symbol associated with the name. If it does, the variable has been declared. If it doesn’t, the variable hasn’t been declared yet, which is a semantic error.

To implement Step 4, we need to make some changes to the symbol table and semantic analyzer:

  1. We need to add a method to our symbol table that will be able to look up a symbol by name.
  2. We need to update our semantic analyzer to look up a name in the symbol table every time it encounters a variable reference.

First, let’s update our SymbolTable class by adding the lookup method that will be responsible for searching for a symbol by name. In other words, the lookup method will be responsible for resolving a variable name (a variable reference) to its declaration. The process of mapping a variable reference to its declaration is called name resolution. And here is our lookup method that does just that, name resolution:

def lookup(self, name):
    print('Lookup: %s' % name)
    symbol = self._symbols.get(name)
    # 'symbol' is either an instance of the Symbol class or None
    return symbol

The method takes a symbol name as a parameter and returns a symbol if it finds it or None if it doesn’t. As simple as that.

While we’re at it, let’s also update our SymbolTable class to initialize built-in types. We’ll do that by adding a method _init_builtins and calling it in the SymbolTable‘s constructor. The _init_builtins method will insert a type symbol for integer and a type symbol for real into the symbol table.

Here is the full code for our updated SymbolTable class:

class SymbolTable(object):
    def __init__(self):
        self._symbols = {}
        self._init_builtins()

    def _init_builtins(self):
        self.insert(BuiltinTypeSymbol('INTEGER'))
        self.insert(BuiltinTypeSymbol('REAL'))

    def __str__(self):
        symtab_header = 'Symbol table contents'
        lines = ['\n', symtab_header, '_' * len(symtab_header)]
        lines.extend(
            ('%7s: %r' % (key, value))
            for key, value in self._symbols.items()
        )
        lines.append('\n')
        s = '\n'.join(lines)
        return s

    __repr__ = __str__

    def insert(self, symbol):
        print('Insert: %s' % symbol.name)
        self._symbols[symbol.name] = symbol

    def lookup(self, name):
        print('Lookup: %s' % name)
        symbol = self._symbols.get(name)
        # 'symbol' is either an instance of the Symbol class or None
        return symbol


Now that we have built-in type symbols and the lookup method to search our symbol table when we encounter variable names (and other names like type names), let’s update the SemanticAnalyzer‘s visit_VarDecl method and replace the two lines where we were manually creating the INTEGER built-in type symbol and manually inserting it into the symbol table with code to look up the INTEGER type symbol.

The change will also fix the issue with that double output of the Insert: INTEGER line we’ve seen before.

Here is the visit_VarDecl method before the change:

def visit_VarDecl(self, node):
    # For now, manually create a symbol for the INTEGER built-in type
    # and insert the type symbol in the symbol table.
    type_symbol = BuiltinTypeSymbol('INTEGER')
    self.symtab.insert(type_symbol)

    # We have all the information we need to create a variable symbol.
    # Create the symbol and insert it into the symbol table.
    var_name = node.var_node.value
    var_symbol = VarSymbol(var_name, type_symbol)
    self.symtab.insert(var_symbol)

and after the change:

def visit_VarDecl(self, node):
    type_name = node.type_node.value
    type_symbol = self.symtab.lookup(type_name)

    # We have all the information we need to create a variable symbol.
    # Create the symbol and insert it into the symbol table.
    var_name = node.var_node.value
    var_symbol = VarSymbol(var_name, type_symbol)
    self.symtab.insert(var_symbol)

Let’s apply the changes to the familiar Pascal program that has only variable declarations:

program SymTab3;
   var x, y : integer;

begin

end.

Download the symtab03.py file that has all the changes we’ve just discussed, run it on the command line, and see that there is no longer a duplicate Insert: INTEGER line in the program output any more:

$ python symtab03.py
Insert: INTEGER
Insert: REAL
Lookup: INTEGER
Insert: x
Lookup: INTEGER
Insert: y


Symbol table contents
_____________________
INTEGER: <BuiltinTypeSymbol(name='INTEGER')>
   REAL: <BuiltinTypeSymbol(name='REAL')>
      x: <VarSymbol(name='x', type='INTEGER')>
      y: <VarSymbol(name='y', type='INTEGER')>

You can also see in the output above that our semantic analyzer looks up the INTEGER built-in type twice: first for the declaration of the variable x, and the second time for the declaration of the variable y.


Now let’s switch our attention to variable references (names) and how we can resolve a variable name, let’s say in an arithmetic expression, to its variable declaration (variable symbol). Let’s take a look at the following sample program, for example, that has an assignment statement x := x + y; with three variable references: x, another x, and y:

program SymTab4;
    var x, y : integer;

begin
    x := x + y;
end.

We already have the lookup method in our symbol table implementation. What we need to do now is extend our semantic analyzer so that every time it encounters a variable reference it would search the symbol table by the variable reference name using the symbol table’s lookup name. What method of the SemanticAnalyzer gets called every time a variable reference is encountered when the analyzer walks the AST? It’s the method visit_Var. Let’s add it to our class. It’s very simple: all it does is look up the variable symbol by name:

def visit_Var(self, node):
    var_name = node.value
    var_symbol = self.symtab.lookup(var_name)


Because our sample program SymTab4 has an assignment statement with arithmetic addition in its right hand side, we need to add two more methods to our SemanticAnalyzer so that it could actually walk the AST of the SymTab4 program and call the visit_Var method for all Var nodes. The methods we need to add are visit_Assign and visit_BinOp. They are nothing new: you’ve seen these methods before. Here they are:

def visit_Assign(self, node):
    # right-hand side
    self.visit(node.right)
    # left-hand side
    self.visit(node.left)

def visit_BinOp(self, node):
    self.visit(node.left)
    self.visit(node.right)


You can find the full source code with the changes we’ve just discussed in the file symtab04.py. Download the file, run it on the command line, and inspect the output produced for our sample program SymTab4 with an assignment statement.

Here is the output on my laptop:

$ python symtab04.py
Insert: INTEGER
Insert: REAL
Lookup: INTEGER
Insert: x
Lookup: INTEGER
Insert: y
Lookup: x
Lookup: y
Lookup: x


Symbol table contents
_____________________
INTEGER: <BuiltinTypeSymbol(name='INTEGER')>
   REAL: <BuiltinTypeSymbol(name='REAL')>
      x: <VarSymbol(name='x', type='INTEGER')>
      y: <VarSymbol(name='y', type='INTEGER')>

Spend some time analyzing the output and making sure you understand how and why the output is generated in that order.

At this point, we have implemented all of the steps of our algorithm for a static semantic check that verifies that all variables in the program are declared before they are used!

Semantic errors

So far we’ve looked at the programs that had their variables declared, but what if our program has a variable reference that doesn’t resolve to any declaration; that is, it’s not declared? That’s a semantic error and we need to extend our semantic analyzer to signal that error.

Take a look at the following semantically incorrect program, where the variable y is not declared but used in the assignment statement:

program SymTab5;
    var x : integer;

begin
    x := y;
end.

To signal the error, we need to modify our SemanticAnalyzer‘s visit_Var method to throw an exception if the lookup method cannot resolve a name to a symbol and returns None. Here is the updated code for visit_Var:

def visit_Var(self, node):
    var_name = node.value
    var_symbol = self.symtab.lookup(var_name)
    if var_symbol is None:
        raise Exception(
            "Error: Symbol(identifier) not found '%s'" % var_name
        )

Download symtab05.py, run it on the command line, and see what happens:

$ python symtab05.py
Insert: INTEGER
Insert: REAL
Lookup: INTEGER
Insert: x
Lookup: y
Error: Symbol(identifier) not found 'y'


Symbol table contents
_____________________
INTEGER: <BuiltinTypeSymbol(name='INTEGER')>
   REAL: <BuiltinTypeSymbol(name='REAL')>
      x: <VarSymbol(name='x', type='INTEGER')>

You can see the error message Error: Symbol(identifier) not found ‘y’ and the contents of the symbol table.

Congratulations on finishing the current version of our semantic analyzer that can statically check if variables in a program are declared before they are used, and if they are not, throws an exception indicating a semantic error!

Let’s pause for a second and celebrate this important milestone. Okay, the second is over and we need to move on to another static semantic check. For fun and profit let’s extend our semantic analyzer to check for duplicate identifiers in declarations.

Let’s take a look at the following program, SymTab6:

program SymTab6;
   var x, y : integer;
   var y : real;
begin
   x := x + y;
end.

Variable y has been declared twice: the first time as integer and the second time as real.

To catch that semantic error we need to modify our visit_VarDecl method to check whether the symbol table already has a symbol with the same name before inserting a new symbol. Here is our new version of the method:

def visit_VarDecl(self, node):
    type_name = node.type_node.value
    type_symbol = self.symtab.lookup(type_name)

    # We have all the information we need to create a variable symbol.
    # Create the symbol and insert it into the symbol table.
    var_name = node.var_node.value
    var_symbol = VarSymbol(var_name, type_symbol)

    # Signal an error if the table alrady has a symbol
    # with the same name
    if self.symtab.lookup(var_name) is not None:
        raise Exception(
            "Error: Duplicate identifier '%s' found" % var_name
        )

    self.symtab.insert(var_symbol)


File symtab06.py has all the changes. Download it and run it on the command line:

$ python symtab06.py
Insert: INTEGER
Insert: REAL
Lookup: INTEGER
Lookup: x
Insert: x
Lookup: INTEGER
Lookup: y
Insert: y
Lookup: REAL
Lookup: y
Error: Duplicate identifier 'y' found


Symbol table contents
_____________________
INTEGER: <BuiltinTypeSymbol(name='INTEGER')>
   REAL: <BuiltinTypeSymbol(name='REAL')>
      x: <VarSymbol(name='x', type='INTEGER')>
      y: <VarSymbol(name='y', type='INTEGER')>

Study the output and the contents of the symbol table. Make sure you understand what’s going on.


Summary

Let’s quickly recap what we learned today:

  • We learned more about symbols, symbol tables, and semantic analysis in general
  • We learned about name resolution and how the semantic analyzer resolves names to their declarations
  • We learned how to code a semantic analyzer that walks an AST, builds the symbol table, and does basic semantic checks


And, as a reminder, the structure of our interpreter now looks like this:


We’re done with semantic checks for today and we’re finally ready to tackle the topic of scopes, how they relate to symbol tables, and the topic of semantic checks in the presence of nested scopes. Those will be central topics of the next article. Stay tuned and see you soon!


Get the edge and stay sharp. Subscribe to Beyond Basics for free and get new posts without missing a beat!


All articles in this series:

Comments

comments powered by Disqus