Let’s Build A Simple Interpreter. Part 6.

Date

Today is the day :) “Why?” you might ask. The reason is that today we’re wrapping up our discussion of arithmetic expressions (well, almost) by adding parenthesized expressions to our grammar and implementing an interpreter that will be able to evaluate parenthesized expressions with arbitrarily deep nesting, like the expression 7 + 3 * (10 / (12 / (3 + 1) - 1)).

Let’s get started, shall we?

First, let’s modify the grammar to support expressions inside parentheses. As you remember from Part 5, the factor rule is used for basic units in expressions. In that article, the only basic unit we had was an integer. Today we’re adding another basic unit - a parenthesized expression. Let’s do it.

Here is our updated grammar:

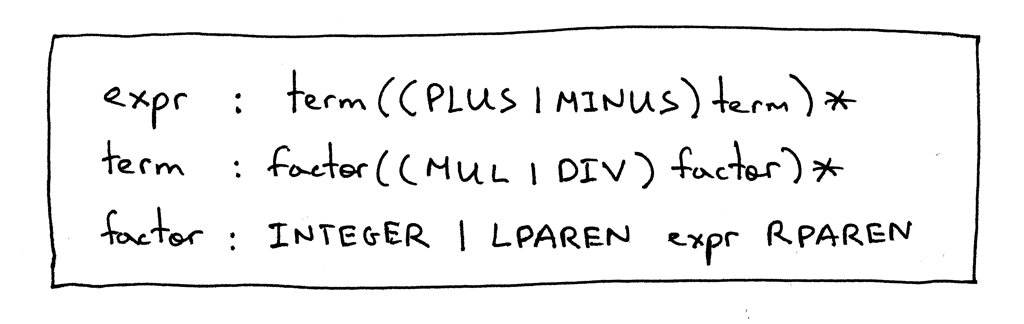
The expr and the term productions are exactly the same as in Part 5 and the only change is in the factor production where the terminal LPAREN represents a left parenthesis ‘(‘, the terminal RPAREN represents a right parenthesis ‘)’, and the non-terminal expr between the parentheses refers to the expr rule.

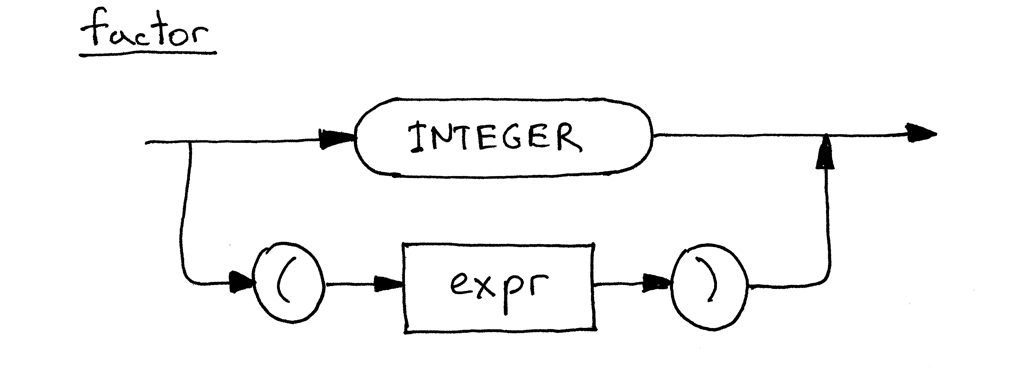
Here is the updated syntax diagram for the factor, which now includes alternatives:

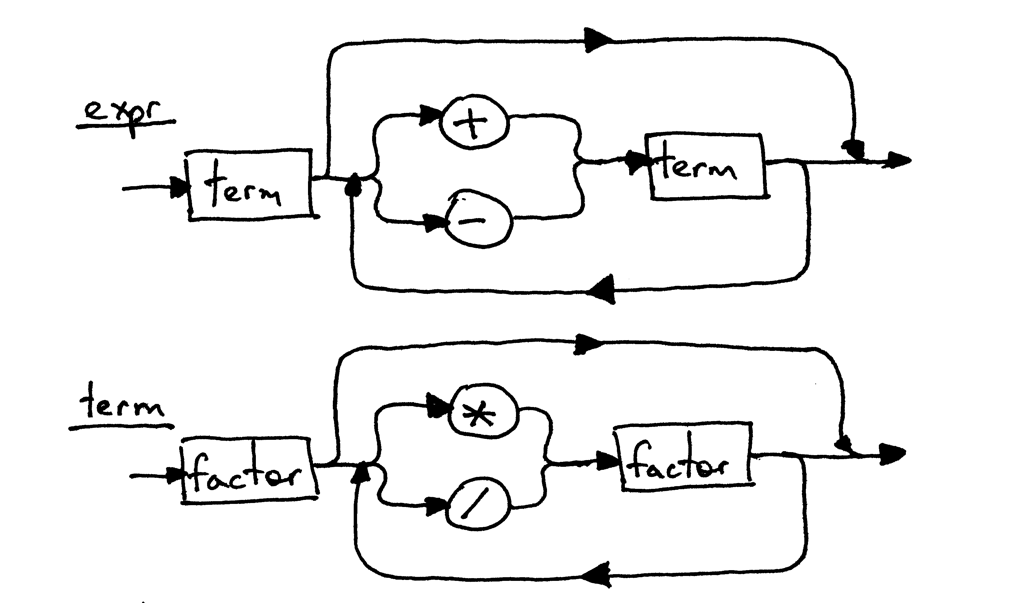
Because the grammar rules for the expr and the term haven’t changed, their syntax diagrams look the same as in Part 5:

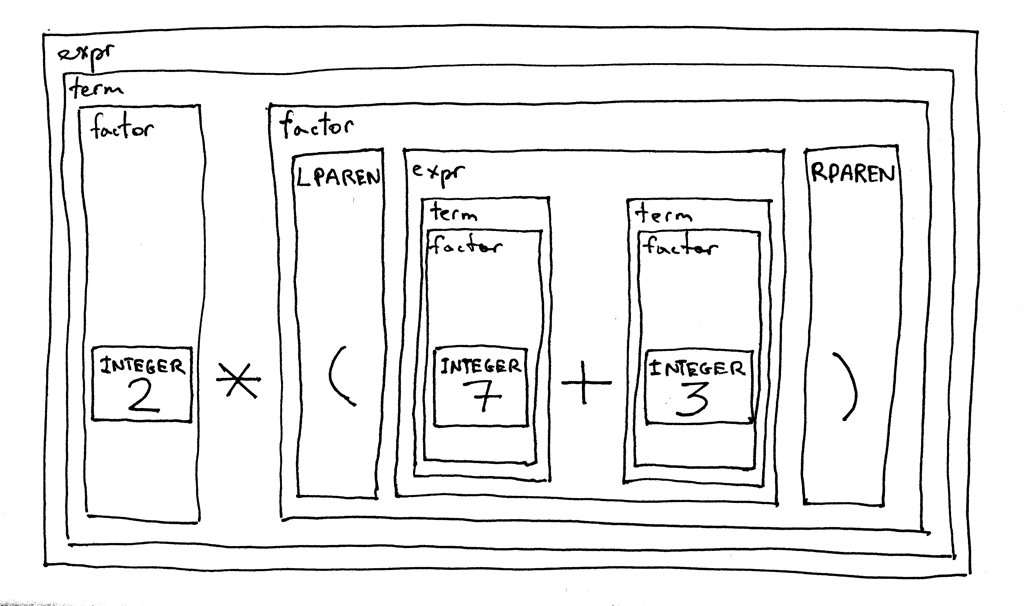
Here is an interesting feature of our new grammar - it is recursive. If you try to derive the expression 2 * (7 + 3), you will start with the expr start symbol and eventually you will get to a point where you will recursively use the expr rule again to derive the (7 + 3) portion of the original arithmetic expression.

Let’s decompose the expression 2 * (7 + 3) according to the grammar and see how it looks:

A little aside: if you need a refresher on recursion, take a look at Daniel P. Friedman and Matthias Felleisen’s The Little Schemer book - it’s really good.

Okay, let’s get moving and translate our new updated grammar to code.

The following are the main changes to the code from the previous article:

  1. The Lexer has been modified to return two more tokens: LPAREN for a left parenthesis and RPAREN for a right parenthesis.
  2. The Interpreter‘s factor method has been slightly updated to parse parenthesized expressions in addition to integers.

Here is the complete code of a calculator that can evaluate arithmetic expressions containing integers; any number of addition, subtraction, multiplication and division operators; and parenthesized expressions with arbitrarily deep nesting:

# Token types
#
# EOF (end-of-file) token is used to indicate that
# there is no more input left for lexical analysis
INTEGER, PLUS, MINUS, MUL, DIV, LPAREN, RPAREN, EOF = (
    'INTEGER', 'PLUS', 'MINUS', 'MUL', 'DIV', '(', ')', 'EOF'
)


class Token(object):
    def __init__(self, type, value):
        self.type = type
        self.value = value

    def __str__(self):
        """String representation of the class instance.

        Examples:
            Token(INTEGER, 3)
            Token(PLUS, '+')
            Token(MUL, '*')
        """
        return 'Token({type}, {value})'.format(
            type=self.type,
            value=repr(self.value)
        )

    def __repr__(self):
        return self.__str__()


class Lexer(object):
    def __init__(self, text):
        # client string input, e.g. "4 + 2 * 3 - 6 / 2"
        self.text = text
        # self.pos is an index into self.text
        self.pos = 0
        self.current_char = self.text[self.pos]

    def error(self):
        raise Exception('Invalid character')

    def advance(self):
        """Advance the `pos` pointer and set the `current_char` variable."""
        self.pos += 1
        if self.pos > len(self.text) - 1:
            self.current_char = None  # Indicates end of input
        else:
            self.current_char = self.text[self.pos]

    def skip_whitespace(self):
        while self.current_char is not None and self.current_char.isspace():
            self.advance()

    def integer(self):
        """Return a (multidigit) integer consumed from the input."""
        result = ''
        while self.current_char is not None and self.current_char.isdigit():
            result += self.current_char
            self.advance()
        return int(result)

    def get_next_token(self):
        """Lexical analyzer (also known as scanner or tokenizer)

        This method is responsible for breaking a sentence
        apart into tokens. One token at a time.
        """
        while self.current_char is not None:

            if self.current_char.isspace():
                self.skip_whitespace()
                continue

            if self.current_char.isdigit():
                return Token(INTEGER, self.integer())

            if self.current_char == '+':
                self.advance()
                return Token(PLUS, '+')

            if self.current_char == '-':
                self.advance()
                return Token(MINUS, '-')

            if self.current_char == '*':
                self.advance()
                return Token(MUL, '*')

            if self.current_char == '/':
                self.advance()
                return Token(DIV, '/')

            if self.current_char == '(':
                self.advance()
                return Token(LPAREN, '(')

            if self.current_char == ')':
                self.advance()
                return Token(RPAREN, ')')

            self.error()

        return Token(EOF, None)


class Interpreter(object):
    def __init__(self, lexer):
        self.lexer = lexer
        # set current token to the first token taken from the input
        self.current_token = self.lexer.get_next_token()

    def error(self):
        raise Exception('Invalid syntax')

    def eat(self, token_type):
        # compare the current token type with the passed token
        # type and if they match then "eat" the current token
        # and assign the next token to the self.current_token,
        # otherwise raise an exception.
        if self.current_token.type == token_type:
            self.current_token = self.lexer.get_next_token()
        else:
            self.error()

    def factor(self):
        """factor : INTEGER | LPAREN expr RPAREN"""
        token = self.current_token
        if token.type == INTEGER:
            self.eat(INTEGER)
            return token.value
        elif token.type == LPAREN:
            self.eat(LPAREN)
            result = self.expr()
            self.eat(RPAREN)
            return result

    def term(self):
        """term : factor ((MUL | DIV) factor)*"""
        result = self.factor()

        while self.current_token.type in (MUL, DIV):
            token = self.current_token
            if token.type == MUL:
                self.eat(MUL)
                result = result * self.factor()
            elif token.type == DIV:
                self.eat(DIV)
                result = result / self.factor()

        return result

    def expr(self):
        """Arithmetic expression parser / interpreter.

        calc> 7 + 3 * (10 / (12 / (3 + 1) - 1))
        22

        expr   : term ((PLUS | MINUS) term)*
        term   : factor ((MUL | DIV) factor)*
        factor : INTEGER | LPAREN expr RPAREN
        """
        result = self.term()

        while self.current_token.type in (PLUS, MINUS):
            token = self.current_token
            if token.type == PLUS:
                self.eat(PLUS)
                result = result + self.term()
            elif token.type == MINUS:
                self.eat(MINUS)
                result = result - self.term()

        return result


def main():
    while True:
        try:
            # To run under Python3 replace 'raw_input' call
            # with 'input'
            text = raw_input('calc> ')
        except EOFError:
            break
        if not text:
            continue
        lexer = Lexer(text)
        interpreter = Interpreter(lexer)
        result = interpreter.expr()
        print(result)


if __name__ == '__main__':
    main()

Save the above code into the calc6.py file, try it out and see for yourself that your new interpreter properly evaluates arithmetic expressions that have different operators and parentheses.

Here is a sample session:

$ python calc6.py
calc> 3
3
calc> 2 + 7 * 4
30
calc> 7 - 8 / 4
5
calc> 14 + 2 * 3 - 6 / 2
17
calc> 7 + 3 * (10 / (12 / (3 + 1) - 1))
22
calc> 7 + 3 * (10 / (12 / (3 + 1) - 1)) / (2 + 3) - 5 - 3 + (8)
10
calc> 7 + (((3 + 2)))
12


And here is a new exercise for you for today:

  • Write your own version of the interpreter of arithmetic expressions as described in this article. Remember: repetition is the mother of all learning.


Hey, you read all the way to the end! Congratulations, you’ve just learned how to create (and if you’ve done the exercise - you’ve actually written) a basic recursive-descent parser / interpreter that can evaluate pretty complex arithmetic expressions.

In the next article I will talk in a lot more detail about recursive-descent parsers. I will also introduce an important and widely used data structure in interpreter and compiler construction that we’ll use throughout the series.

Stay tuned and see you soon. Until then, keep working on your interpreter and most importantly: have fun and enjoy the process!


Here is a list of books I recommend that will help you in your study of interpreters and compilers:

  1. Language Implementation Patterns: Create Your Own Domain-Specific and General Programming Languages (Pragmatic Programmers)

  2. Writing Compilers and Interpreters: A Software Engineering Approach

  3. Modern Compiler Implementation in Java

  4. Modern Compiler Design

  5. Compilers: Principles, Techniques, and Tools (2nd Edition)


Get the edge and stay sharp. Subscribe to Beyond Basics for free and get new posts without missing a beat!


All articles in this series:

Comments

comments powered by Disqus